Transformer的位置编码
一文读懂Transformer模型的位置编码——学习笔记
Transformer 为什么需要位置编码?
- 单词在文本中的位置以及排列顺序对于文本语义的表达十分重要。整个文本的段落含义很可能随着一个单词在句子的位置或排列顺序不同而产生偏差。
- RNN 本身就是个顺序结构,包含了词在序列中的位置信息,因此不需要单独对序列进行位置编码。而 transformer 用 attention 完全取代 RNN 结构后,词序信息就会丢失,模型没有办法知道每个词在文本中的相对和绝对的位置信息。因此,有必要把词序信号加到词向量上帮助模型学习这些信息,所采用的方法即称为位置编码。
位置编码
概念
位置编码(Positional Encoding)是一种用词的位置信息对序列中的每个词进行二次表示的方法。Transformer模型本身不具备像RNN那样的学习词序信息的能力,需要主动将词序信息喂给模型。那么,模型原先的输入是不含词序信息的词向量,位置编码需要将词序信息和词向量结合起来形成一种新的表示输入给模型,这样模型就具备了学习词序信息的能力。
实现方法
一种好的位置编码方案需要满足以下几条要求:
- 它能为每个时间步输出一个独一无二的编码;
- 不同长度的句子之间,任何两个时间步之间的距离应该保持一致;
- 模型应该能毫不费力地泛化到更长的句子。它的值应该是有界的;
- 它必须是确定性的。
方法一:分配一个0到1之间的数值给每个时间步,其中,0表示第一个词,1表示最后一个词。
存在的问题:无法知道在一个特定区间范围内到底存在多少个单词。换句话说,不同句子之间的时间步差值没有任何的意义。如图,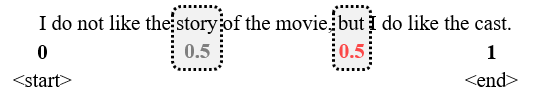
将 0 和 1 分别分配给第一个词和最后一个词,但关于内部数值的分配我们不得而知,0.5对应的时间步(词位置)可能在句子一半靠前的位置,也可能在一半靠后的位置,即不会完全对应于句子中心,因此,你无法确定在某个区间范围内包含了多少个单词。
方法二:为了解决上述方法任意两个时间步空间距离相等的情况,线性分配一个数值给每个时间步。也就是,1分配给第一个词,2分配给第二个词,以此类推,这样各个词间的距离就均保证为1且相等。
存在的问题:随着文本长度增加,这些数值会变得非常大,此外,模型也会遇到一些比训练中的所有句子都要长的句子。数据集中不一定在所有数值上都会包含相对应长度的句子,也就是模型很有可能没有看到过任何一个这样的长度的样本句子,这会严重影响模型的泛化能力。如图,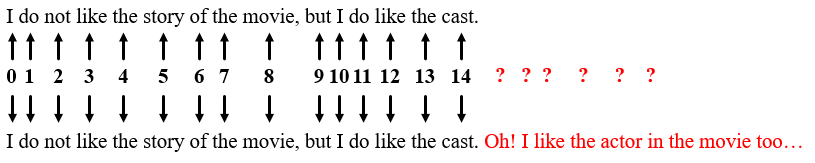
上述方法均存在一定的问题,没有满足位置编码方案的要求。Transformer 则提出了一种基于三角函数的位置编码方式,很好的解决了上述问题,我们将具体分析它是如何解决这些问题的。
Position Encoding
- Position Encoding 编码不是单一的一个数值,而是包含句子中特定位置信息的 d 维向量 (一个位置对应一个 d 维向量)。
- Position Encoding 编码没有整合进模型,而是用这个向量让每个词具有它在句子中的位置的信息。换句话说,通过注入词的顺序信息来增强模型输入 (Position Encoding + Input Embedding)。
t位置信息 -> d维向量
假设文本输入为一个长度为 n 的序列,我们用 t 来表示第 t 个词在文本中的位置。根据上述信息,我们可以将文本中一个特定位置信息表示为一个 d 维向量,因此,我们将 t 所对应的 d 维向量记为 $p_t\in R^d$,其对应的函数映射我们记为$f:N\rightarrow R^d$,即有 $p_t=f(t)$,其中 $f()$函数映射计算第 i 个维度的 $p_t^i$ 的具体公式如下,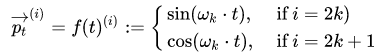
其中,$k\in [0,(d_{model} - 1)/2]$,频率$w_k=1/(10000^{2k/d})$,$i\in [1,d_{model}]$表示向量的第 i 维。频率沿向量维度减小,且 d 可被 2 整除。
因此,遍历 k 计算各个维度,每个 t 对应的位置编码 $p_t$可以表示为如下所示,向量长度为 d,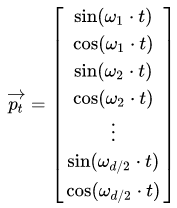
其中,将所有输入序列的编码向量(n个d维向量)进行排列,可得到如下图像,其表示了长度为200、维度为150的序列转置后的位置矩阵PE,红线指输入序列的第 i 个维度。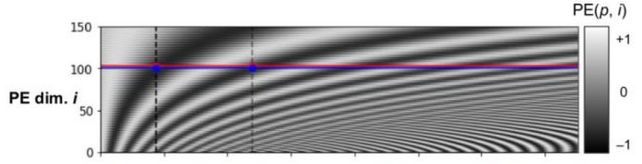
Position Encoding + Input Embedding
位置编码方法已经有了,那如何让每个词具有它们的位置信息?原始论文将位置编码加到模型输入之上。也就是,对于句子里的每个词,计算其对应的词嵌入,然后按照下面的方法喂给模型: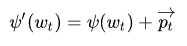
为了保证这种相加操作正确,需要让位置向量(PE)的维度等于词向量(WE)的维度,即 $d_{PE}=d_{WE}$。假设某位置 t 的词被 embedding 编码为了 4 维向量,那么执行相加操作的时候,必须也要保证位置编码后的 p 向量维度也为 4,这也就解释了为什么上述 $p_t\in R^{d_{model}}$的原因。
举例

本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!