attention 机制详解

attention

参考链接：
Self-Attention和Transformer
拆 Transformer 系列二：Multi- Head Attention 机制详解
目前主流的attention方法都有哪些？

Attention 实现机制(本质)

Attention 机制实质上就是一个寻址过程：
通过给定一个任务相关的查询 Query 向量 Q，通过计算与 Key 的注意力分布并附加在 Value 上，从而计算 Attention Value。
其中涉及到了注意力打分机制和注意力概率分布作用过程。

What is Q, K, V ?

字面理解

Q: Question，问题
K：Key，关键字
V：Value，值
模型抛出一个问题（被查询的对象），根据辅助的关键字信息，得到两者间的相似度关系，经过归一化（softmax）后。作用在目标值上，即实现了根据前者相似度来影响目标的权重分布。
前一句体现了注意力的打分机制，后一句则体现了利用概率影响 Value 的作用机制。

本质：根据注意力的打分机制，计算两个对象内部的相似关系，并将其作用于目标中。

关于注意力的整个过程，形象理解如下(转自Self-Attention和Transformer)：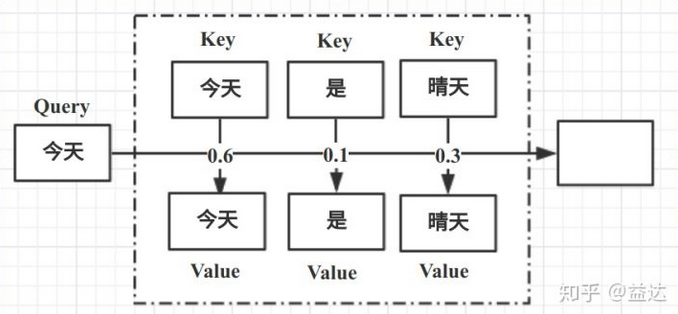

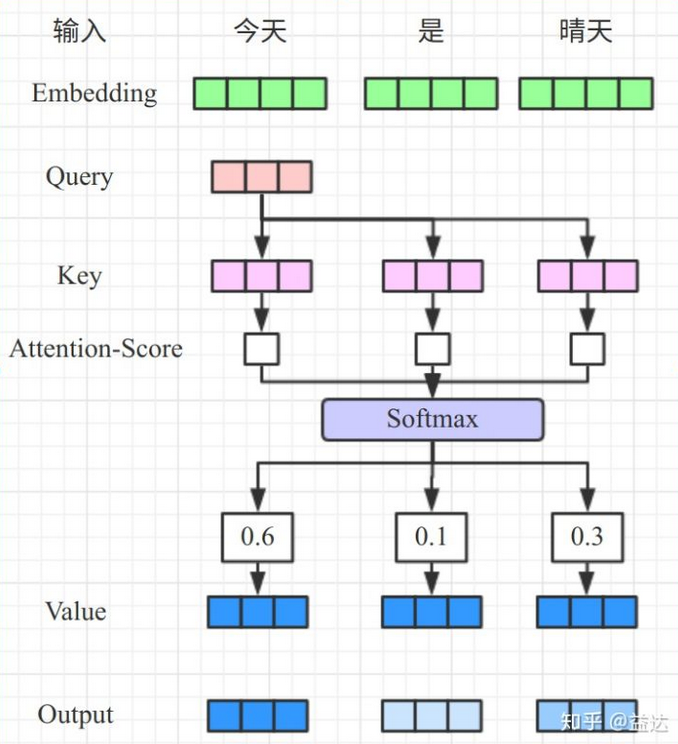
注意力打分机制

$\alpha_i=softmax(s(x_i,q))$，其中$\alpha$为注意力概率分布，$s(x_i,q)$为注意力打分机制。

常用的注意力打分机制有以下几种：

  1. 加性模型：$s(x_i,q)=v^Ttanh(Wx_i+Uq)$
  2. 点积模型：$s(x_i,q)=x_i^Tq$
  3. 缩放点积模型：$s(x_i,q)=(x_i^Tq)/\sqrt{d_k}$
  4. 双线性模型：$s(x_i,q)=x_i^TWq$

$attention(V)=\sum_{i=1}^N\alpha_iV_i=\alpha V$

注意事项

  1. 缩放点积模型能防止点积结果过大导致 softmax 梯度过小，反向传播困难的情况。缩放点积模型相较于点积模型更好。
  2. 点积模型及缩放点积模型需要保证矩阵的点积规则，及$(N\times H)\cdot(H\times V)$，在 self-attention 中，由于 Q 和 K 矩阵行数相同，因此仅需要注意最后得到结果的矩阵大小。假设 Q 长度为4，embed_dim 为6的序列($6\times 4$)，K 大小为$6\times 3$，那么就不能硬套上述点积公式，因为我们目标是获得 Q 和 K 的相似关系，即最后矩阵大小为 $3\times 4$，所以我们注意力打分的点积模型为 $s(x,q)=K^TQ$。
  3. 若 Q，K 的矩阵点积无法满足点积规则，则可以用双线性模型或者加性模型，其中 W，U 的作用就是将两者拉到同一维度上进行矩阵运算。

补充

阅读了目前主流的attention方法都有哪些？，特来对注意力打分机制的公式做一个补充。

注意力机制可以分为三步：一是信息输入；二是计算注意力分布α；三是根据注意力分布α 来计算输入信息的加权平均。

  1. 信息输入：$X=[x_0,…,x_N]$表示N 个输入信息。注意思考此处$x_i$的编码向量为：列向量 (对于后续公式的理解很重要!!!)
  2. 注意力分布计算：令Key=Value=X，则可以给出注意力分布，$\alpha_i=softmax(s(k_i,q))=softmax(s(x_i,q))$。
  3. 根据打分机制计算注意力得分系数：
    加性模型：$s(x_i,q)=v^Ttanh(Wx_i+Uq)$
    点积模型：$s(x_i,q)=x_i^Tq$
    缩放点积模型：$s(x_i,q)=(x_i^Tq)/\sqrt{d_k}$
    双线性模型：$s(x_i,q)=x_i^TWq$
  4. 信息加权：注意力分布 $\alpha_i$ 可以解释为在上下文查询q时，第i个信息受关注的程度，采用一种“软性”的信息选择机制对输入信息X进行编码为，$attention(q,X)=\sum_{i=1}^N\alpha_iX_i$，用矩阵乘法表示为 $V(K^TQ)$，注意列向量是右乘的形式，若以行向量计算则为左乘形式$(QK^T)V$。

软性注意力机制（soft Attention）

软性注意力机制有两种：普通模式（Key=Value=X）和键值对模式（Key！=Value）: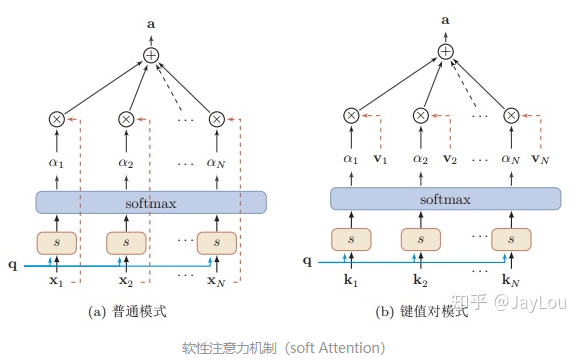

疑点

在学习 transformer 过程中一直有个疑问，在点积模型中，$s(x_i,q)=x_i^Tq$，可知，$q$对应的是Q，而$x$对应的是K，可是在transformer中，公式是$QK^T$，按理来说两者表达的是同一个意思，但是矩阵左乘和右乘还是有一定区别的，故对此做了相应的思考，最终得出一个解释：
在$s(x_i,q)=x_i^Tq$中，$x_i$是以列向量形式表示的！即假设$x_i$是一个embed_dim=4的单词，那么实际上它的向量形式表示为$(4\times 1)$。
所以：
向量尽量以列向量表示！！！
向量尽量以列向量表示！！！
向量尽量以列向量表示！！！
完毕！

补充2

之前一直没有弄明白 Query, Key, Value 是怎么区分的，上述补充我们已知 Key = Value 和 Key != Value 的情况，即 Key 和 Value 在某种情况下是互通的，但是 Query 又怎么区分呢？什么可以作为 Query ？
参考自然语言处理中的Attention机制总结

attention 通用定义

按照Stanford大学课件上的描述，attention的通用定义如下：

  1. 给定一组向量集合values，以及一个向量query，attention机制是一种根据该query计算values的加权求和的机制。
  2. attention的重点就是这个集合values中的每个value的“权值”的计算方法。

Query: 目标向量

参考链接：attention机制
在自然语言处理中，我们通常将目标作为 Query ，辅助信息作为 Key 和 Value。
例如在英译汉中，我们已知英语，需要对汉语做权值重新分配，则将汉语词向量作为 Query = “老师早上好”，将英语作为 (Key / Value) = “Goodmorning teacher”，设 embedding dim 大小为 3，Query 向量大小为 $3\times 5$，(Key / Value) 向量大小为 $3\times 2$，计算相似度 $K^TQ = (2\times 5)$，将相似度作用于 Value 上，得到 $V(K^TQ)=(3\times 5)$。可以看到最终输出的向量大小与 Query 保持一致，这也是为什么将 Query 作为自然语言处理目标向量的原因，因为其根据 Key 调整的是 Query 的权重分布。