回溯

回溯算法入门级详解
回溯法: 采用试错思想, 尝试分步解决一个问题; 在分步解决问题的过程中, 当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候, 它将取消上一步甚至是上几步的计算, 再通过其它的可能的分步解答再次尝试寻找问题的答案; 回溯法通常用最简单的递归方法来实现, 在反复重复上述的步骤后可能出现两种情况:

找到一个可能存在的正确的答案；
在尝试了所有可能的分步方法后宣告该问题没有答案;

深度优先搜索算法(DFS): 一种用于遍历或搜索树或图的算法; 该算法会尽可能深的搜索树的分支; 当结点 v 的所在边都己被探寻过, 搜索将回溯到发现结点 v 的那条边的起始结点; 这一过程一直进行到已发现从源结点可达的所有结点为止; 如果还存在未被发现的结点, 则选择其中一个作为源结点并重复以上过程, 整个进程反复进行直到所有结点都被访问为止;

回溯法是基于深度优先搜索思想, 通过遍历实现; 因此, 回溯法也是一种暴力解法, 我们可以通过剪枝, 在遍历过程中将绝对不符合条件的分支即时剪去, 避免无意义的遍历, 从而降低回溯的成本;

回溯与动态规划的区别
共同点
用于求解多阶段决策问题; 多阶段决策问题即:

求解一个问题分为很多步骤（阶段）;
每一个步骤（阶段）可以有多种选择;

不同点

动态规划用于求解问题的最优解;
回溯算法可以搜索得到所有的方案(包括最优解), 但是本质上它是一种遍历算法, 时间复杂度很高;

回溯的状态栈管理

每一个节点表示了求解排列组合问题的不同的阶段, 称之为「状态」;
「状态重置」: 将”状态变量”设置成为和先前一样, 在回到上一层节点的过程中, 需要撤销上一次的选择;
借助栈空间, 保存所需要的状态变量: 遍历往下深入时, 状态变量在状态栈尾部追加, 回退时, 撤销上一次的选择，即从栈尾部弹出状态变量; 全局只需维护一个状态栈;
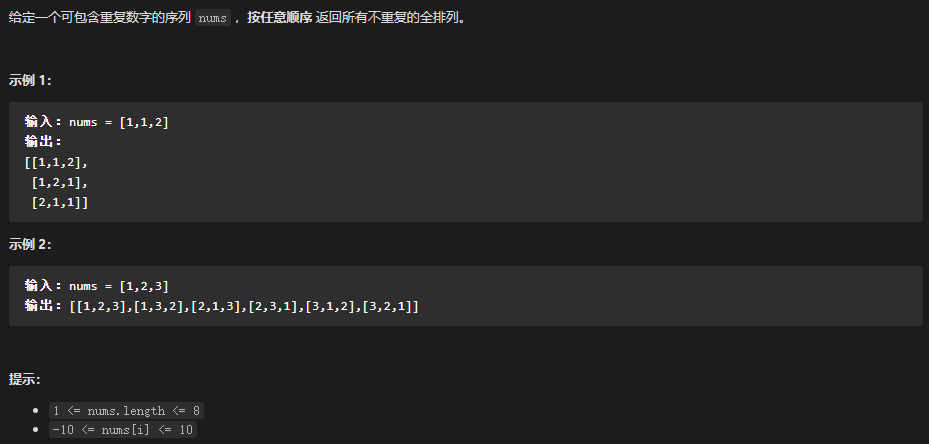
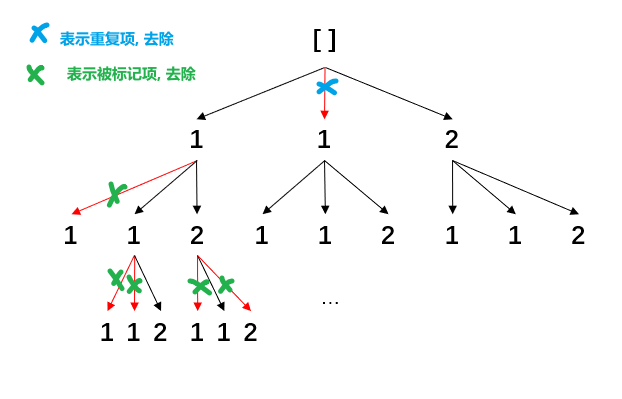
一般来说, 我们仅需要维护一个保存节点的状态栈即可, 但在明确不准重复遍历已遍历节点的场景, 我们可以用一个布尔数组 used 标记已遍历的节点, 详细使用见全排列Ⅱ;

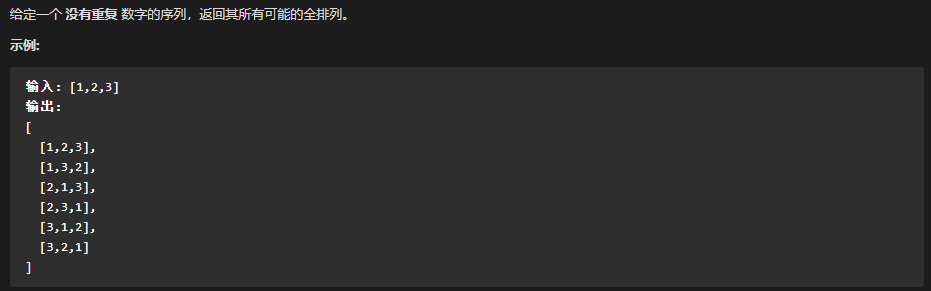
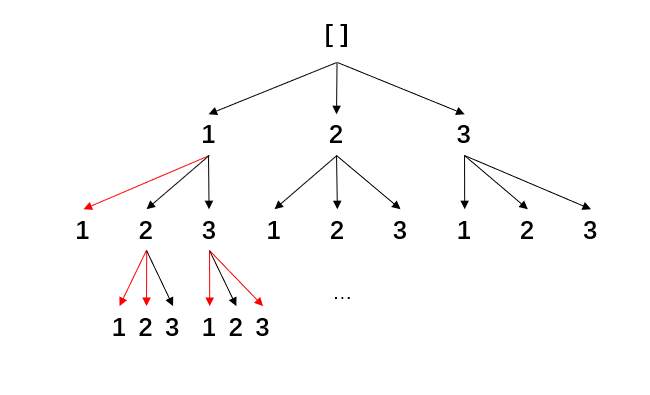
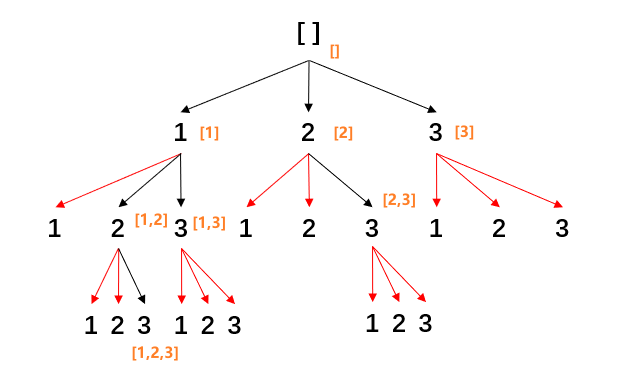
回溯代码实现思路

画树形图 (明确递归结构, 递归出口, 以及剪枝部分)

function xxx(arr) {
  数组与处理 (数组长度, 数组排序...)

  声明变量存储组合结果

  function backTrack(状态栈) {
    if (递归出口条件) {
      存储结果(注意引用类型要克隆)
      递归结束
    }

    for (... 循环遍历当前节点下所有组合 ...) {
      // 回溯操作的关键: 维护一个状态栈, 每次遍历时入栈, 在下一次遍历前出栈, 回溯到同一层节点;
      栈入
      backTrack(...)
      栈出
    }
  }

}

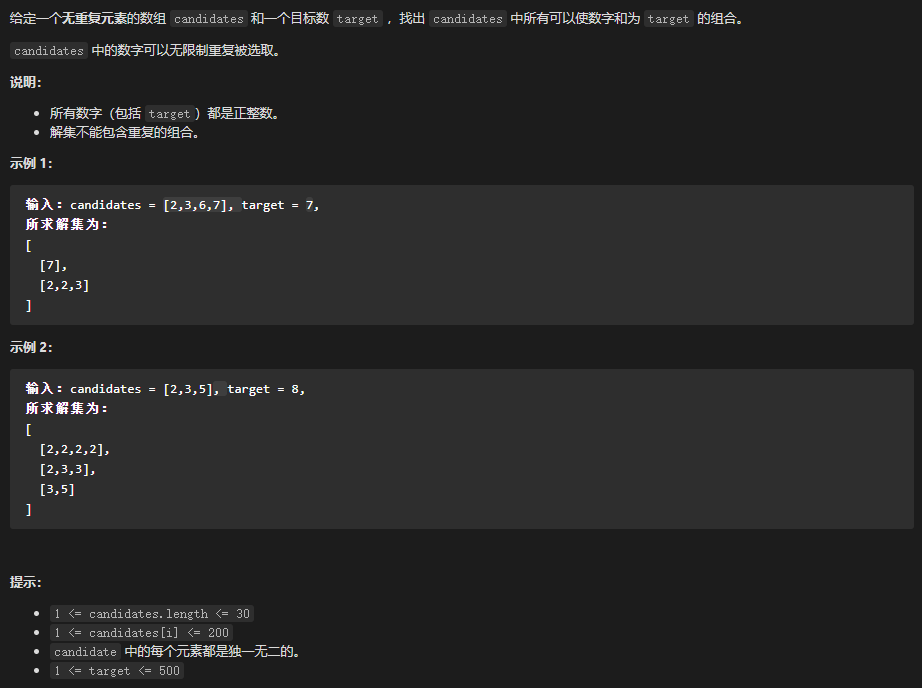
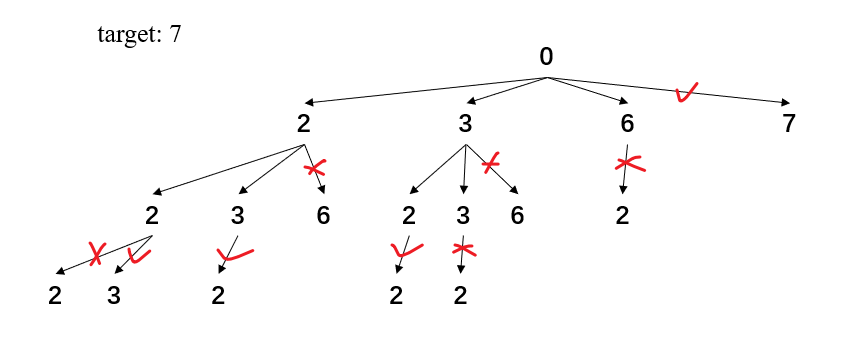
39 - 组合总和

LeetCode题目地址

题解
树形图:

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum = function (candidates, target) {
  // 数组排序
  candidates = candidates.sort((a,b)=>a-b);
  // 结果数组
  let res = [];

  // 递归函数
  // curSum: 当前总和
  // combList: 当前组合列表
  // start: 遍历的节点(去重)
  function backTrack (curSum, combList, start) {
    // 递归出口
    if (curSum >= target) {
      // 若符合条件, 添加当前组合至结果数组
      // (注意此处为克隆, combList 既存储当前组合又是一个状态栈)
      // (直接存储只保留其引用地址, 最终结果会是 [], 因为状态栈最终会回溯到根节点)
      curSum === target && res.push(combList.slice())
      return;
    }
    // 遍历当前层节点
    for (let i=start; i<candidates.length; i++) {
      // 状态栈入栈
      combList.push(candidates[i]);
      // 递归(进入下一层, 下层遍历基于上层节点开始遍历, 达到去重的目的)
      backTrack(curSum + candidates[i], combList, i)
      //状态栈出栈(状态重置到当前层, 遍历当前层其他节点)
      combList.pop();
    }
  }

  backTrack(0, [], 0);

  return res;
};

上述代码实现了回溯的一个基本操作, 即通过递归和遍历实现对每一层节点的判断, 同时维护一个状态栈, 实现回溯算法最关键的状态重置; (回溯是由递归 + 遍历 + 状态栈共同实现的, 本质是递归, 遍历是搜索各节点的手段, 状态栈是状态重置的关键)
本题剪枝思想体现在递归出口处, 当求和结果大于目标值时, 直接终止递归达到剪枝的目的

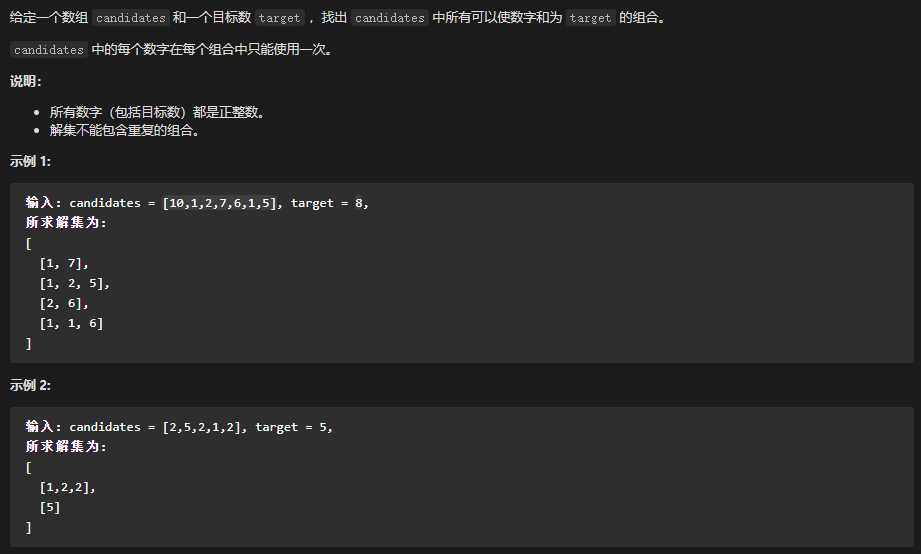
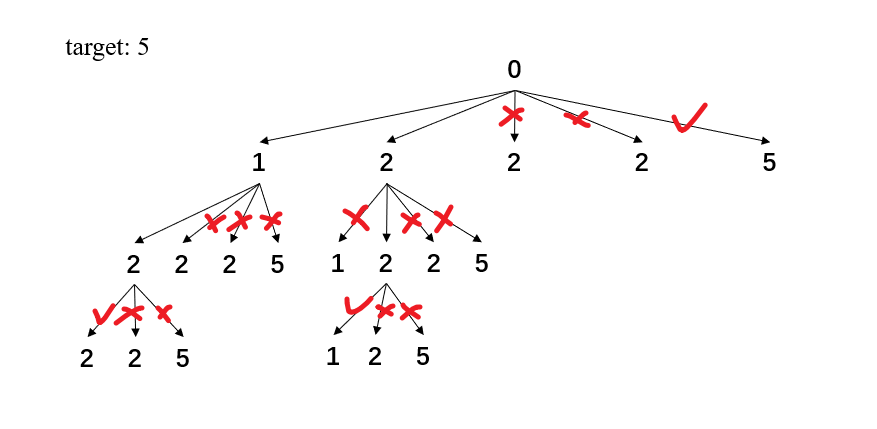
40 - 组合总和 Ⅱ

LeetCode题目地址

题解
与”39-组合总和”不同点在于去重;
树形图

解法一

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function (candidates, target) {
  candidates = candidates.sort((a, b) => a - b);
  const lens = candidates.length;
  const res = [];

  // curCandidates: 该层所遍历的数组
  function backTrack(curSum, combList, curCandidates) {
    if (curSum >= target) {
      curSum === target && res.push(combList.slice());
      return;
    }

    for (let i = 0; i < curCandidates.length; i++) {
      // 若当前节点与前一个节点相同, 会重复, 跳过该节点;
      if (i > 0) {
        while (curCandidates[i] === curCandidates[i - 1]) i++;
      }
      // 维护状态入栈
      combList.push(curCandidates[i]);
      // 下一层遍历的数组不包含当前层已遍历的节点, 因此传入子序列作为新的遍历数组;
      backTrack(curSum + curCandidates[i], combList, curCandidates.slice(i + 1));
      // 出栈
      combList.pop();
    }
  }

  backTrack(0, [], candidates.slice())

  return res;
};

解法二

/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
var combinationSum2 = function (candidates, target) {
  candidates = candidates.sort((a, b) => a - b);
  const lens = candidates.length;
  let res = [];

  // start: 当前层开始遍历的节点索引
  function backTrack(start, curSum, combList) {
    if (curSum >= target) {
      curSum === target && res.push([...combList]);
      return;
    }
    // 从树形图可知, 每层递归遍历, 是从上一个节点后一节点开始的, 因此我们递归遍历下层时, 传入开始索引的位置 (start + 1)
    for (let i = start; i < lens; i++) {
      if (i > start && candidates[i] === candidates[i - 1]) continue;
      combList.push(candidates[i]);
      backTrack(i + 1, curSum + candidates[i], combList);
      combList.pop();
    }
  }

  backTrack(0, 0, []);

  return res;
};

46 - 全排列

LeetCode题目地址

题解
树形图

解法一

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
  nums = nums.sort((a, b) => a - b);
  const lens = nums.length;
  let res = [];

  function backTrack(depth, combList) {
    // 递归出口
    if (depth === lens) {
      res.push(combList.slice());
      return;
    }

    for (let num of nums) {
      // 所有被访问过的节点跳过;
      if (combList.includes(num)) continue;
      // 入栈
      combList.push(num);
      // 遍历下一层, 同时传入当前状态栈(状态栈同时还起到标记已访问节点的作用);
      backTrack(depth + 1, combList);
      // 出栈
      combList.pop()
    }
  }

  backTrack(0, []);

  return res;
};

解法二

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function (nums) {
  nums = nums.sort((a, b) => a - b);
  let res = [];
  const lens = nums.length;

  function backTrack(combList, used = new Array(lens).fill(false)) {
    if (combList.length === lens) {
      res.push([...combList]);
      return;
    }

    for (let i = 0; i < lens; i++) {
      // 维护一个标记栈, 若节点被访问过则将标记栈对应位置置为 true 且每层遍历判断;
      if (used[i]) continue;
      
      combList.push(nums[i]);
      // 标记入栈
      used[i] = true;
      backTrack(combList, used);
      combList.pop();
      // 标记出栈
      used[i] = false;
    }
  }

  backTrack([]);

  return res;
};

47 - 全排列Ⅱ(布尔数组标记去重)

LeetCode题目地址

题解
树形图

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permuteUnique = function (nums) {
  let res = [];
  // 维护一个布尔数组, 标记已遍历的节点
  let used = new Array(nums.length).fill(false);
  nums = nums.sort((a, b) => a - b);

  function backTrack(depth, combList) {
    if (depth === nums.length) {
      res.push(combList.slice());
      return;
    }

    for (let i = 0; i < nums.length; i++) {
      if (used[i]) continue;
      // 注意此处 !used[i-1], 重复项剪枝在被选项剪枝之后, 因此若被选项已被剪枝, 即时该节点重复仍然可以遍历;
      if ((i > 0 && nums[i] === nums[i - 1]) && !used[i-1]) continue;
      combList.push(nums[i]);
      // 标记该节点
      used[i] = true;
      backTrack(depth + 1, combList);
      combList.pop()
      // 回退该节点标记, 进行同层下一个节点遍历
      used[i] = false;
    }
  }

  backTrack(0, []);

  return res;
};

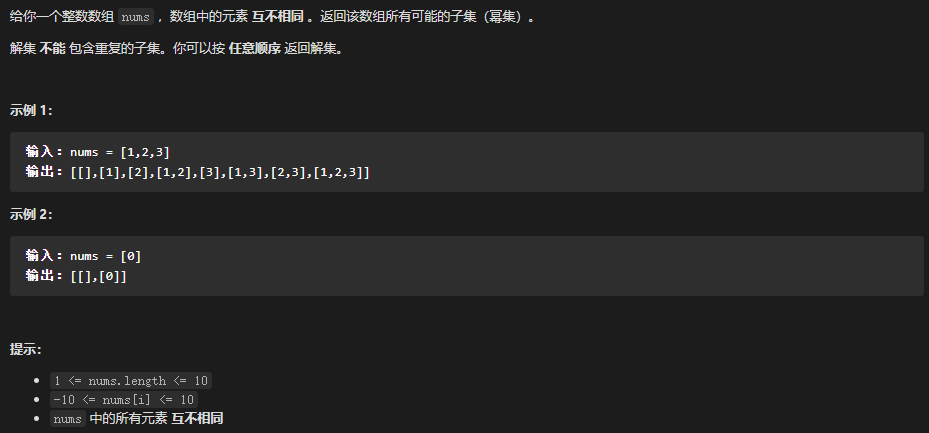
78 - 子集 (遍历索引去重)

LeetCode题目地址

题解
树形图
从树形图中, 我们可以看出, 子集组合需要在每次遍历时就添加进结果数组, 每次向下遍历时, 遍历节点均不包括上一节点之前的所有节点, 因此控制索引去重;

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsets = function (nums) {
  nums = nums.sort((a, b) => a - b);
  const lens = nums.length;
  let res = [[]];

  // start: 每次遍历开始位置
  function backTrack(start, combList) {
    if (combList.length === lens) return;

    for (let i = start; i < lens; i++) {
      combList.push(nums[i]);
      // 在遍历时添加每次遍历的结果
      res.push([...combList]);
      // 从树形图可知, 每次遍历不能包含遍历过的节点, 因此记录每次遍历的索引, 下层遍历从这之后遍历;
      backTrack(i+1, combList);
      combList.pop();
    }
  }

  backTrack(0, []);
  return res;
};

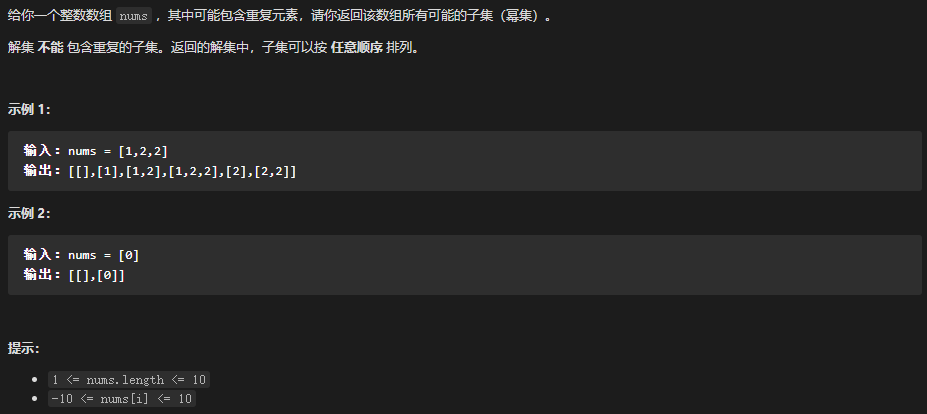
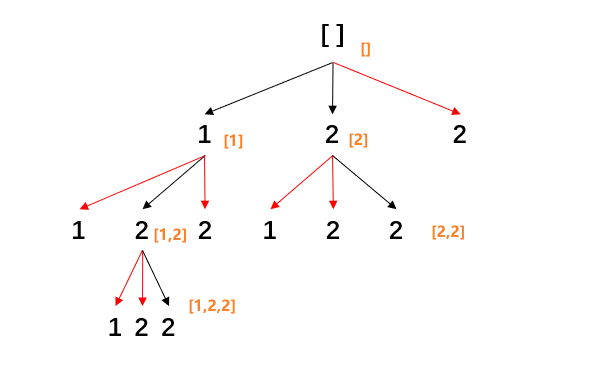
90 - 子集Ⅱ (遍历索引去重)

LeetCode题目地址

题解
树形图
与 78-子集区别在于: 子集Ⅱ需要进一步去重重复的元素, 即后一个遍历节点不能与前一个节点相同 (若前一个节点没有被剪枝的化);

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var subsetsWithDup = function (nums) {
  const lens = nums.length;
  let res = [[],];
  nums = nums.sort((a, b) => a - b);

  function backTrack(start, combList) {
    if (combList.length === lens) return;

    // 与78子集相比, 多了一个后续重复节点的判断
    // 请认真研究基于 start 索引去重和基于 used 标记栈去重的区别;
    for (let i = start; i < lens; i++) {
      if (i > start && nums[i] === nums[i - 1]) continue;
      combList.push(nums[i]);
      res.push([...combList]);
      backTrack(i + 1, combList);
      combList.pop();
    }
  }

  backTrack(0, []);

  return res;
};

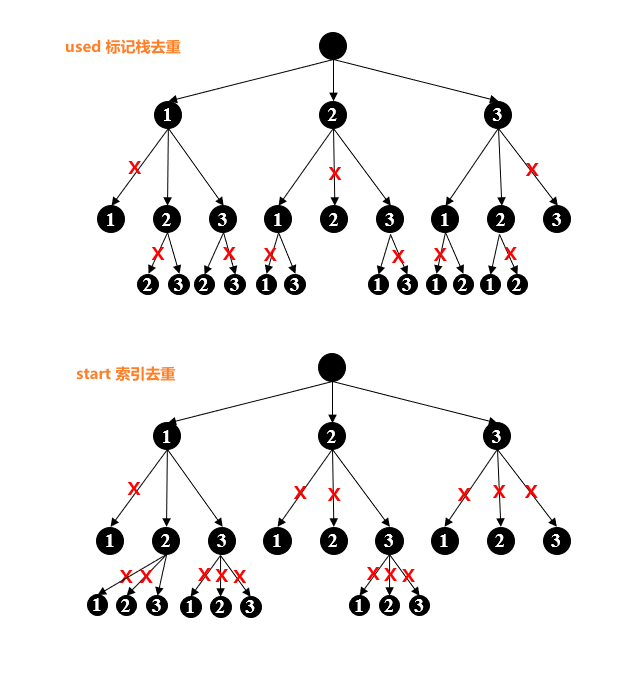
start 索引去重 & used 标记栈去重: 索引去重会删除上一节点之前(具体细节可调整)的所有节点, 删除部分相对于遍历数组是连续的; 标记栈去重则是删除当前遍历分支上之前的节点, 删除部分相对于遍历数组不是连续的;

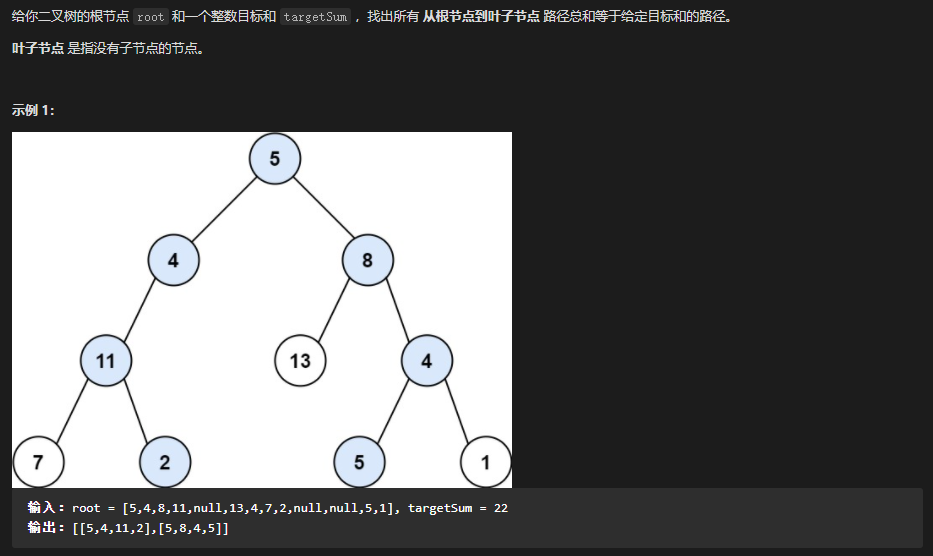
113 - 路径总和Ⅱ

LeetCode题目地址

题解
树形图见示例

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number[][]}
 */
var pathSum = function (root, targetSum) {
  let res = [];
  // 边界条件
  if (!root) return [];

  function backTrack(curSum, combList, curNode) {
    curSum += curNode.val;
    combList.push(curNode.val);
    if (curNode.left || curNode.right) {
      curNode.left && backTrack(curSum, combList, curNode.left);
      // curSum 值还是这层递归的值(原始类型), combList 是引用类型, 被上行递归改变了, 因此需要末尾回溯, 使得上行递归结束后重置到本层递归的 combList;
      curNode.right && backTrack(curSum, combList, curNode.right);
    } else {
      // 递归出口: 当左子节点和右子节点都为 null 时, 该节点为叶子节点;
      curSum === targetSum && res.push([...combList]);
    }
    // 不需要回溯 curSum
    combList.pop();
  }

  backTrack(0, [], root);

  return res;
};

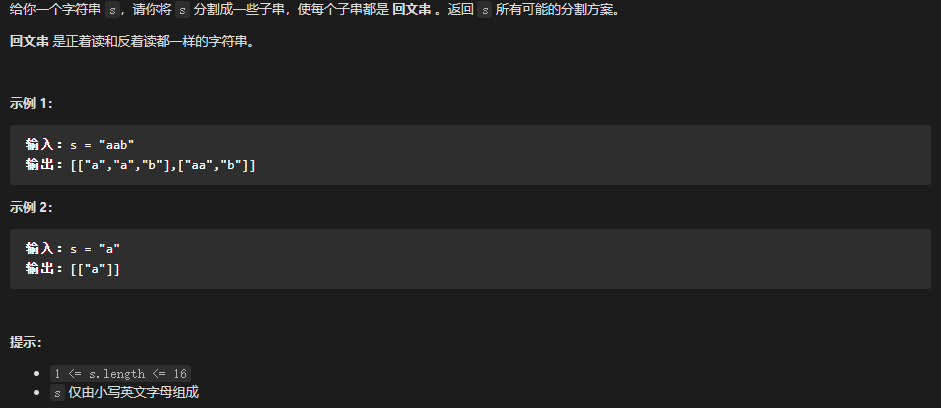
131 - 分割回文串 (涉及回溯和回文串动态规划)

LeetCode题目地址

题解
树形图

/**
 * @param {string} s
 * @return {string[][]}
 */
var partition = function (s) {
  const lens = s.length
  let res = []
  let d = Array.from({ length: lens }, () => new Array(lens).fill(false))

  // 首先标记回文串, 相当于建立了回文串哈希表, 便于查找;
  for (let i = lens - 1; i >= 0; i--) {
    for (let j = i; j < lens; j++) {
      d[i][j] = s[i] === s[j] && (j - i < 2 || d[i + 1][j - 1])
    }
  }

  function backTrack(start, combList) {
    // 递归出口: 遍历完字符串则退出递归
    if (start === lens) {
      res.push([...combList])
      return;
    }
    for (let i = start; i < lens; i++) {
      // 判断组合是否为回文串
      if (!d[start][i]) continue;
      // 是回文串则添加至栈
      combList.push(s.substring(start, i + 1))
      backTrack(i + 1, combList);
      combList.pop();
    }
  }

  backTrack(0, [])

  return res;
};

难点:
回文串哈希表建立: 判断一个字符串是否为回文串, 可判断其两端字符是否相等, 再判断其去除两端后的子字符串是否为回文串, 动态规划公式建立如下:
d[i][j] = s[i] === s[j] && d[i+1][j-1], 因为 i+1 <= j-1, 因此边界条件为 j - i >= 2;
d[i][j] = s[i] === s[j] && j-i < 2;
实现动态规划时, 我们用于二维数组存放结果, 若为 true 表示该二维数组对应下标的字符串是回文串;
二维数组创建方法: Array.from({length: lens}, ()=>new Array(lens)), 即将一个类数组转为数组, 并对类数组内所有元素执行第二参数;
动态规划遍历时, 我们需要先解决最小子问题, 即我们在计算 d[i][j] 之前需要知道 d[i+1][j-1] 的值; 因此我们从后向前遍历, 每次起始遍历时, j === i, 然后逐步扩展;

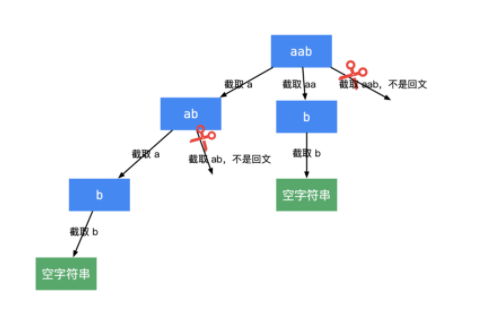
回溯中, 我们将组合是否为回文串作为剪枝条件, 每次递归判断剩余字符的有序组合(例如 ‘aab’ 的有序组合为 ‘a’, ‘aa’, ‘aab’);

算法

数据结构算法面试

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议，转载请注明出处！

ES6篇 - Iterator 上一篇

前端面经下一篇

算法篇 - 回溯

回溯