算法篇 - 二分查找

最佳题解(位于 leetcode 35-搜索插入位置):
写对二分查找不能靠模板,要理解加练习

二分查找

把待搜索区间分成两个部分(核心思想)

二分查找能实现时间复杂度 nlogn 的关键在于: 其利用单调性(绝大多数二分查找问题利用的是单调性, 也有一些例外)或者题目本身蕴含的可以逐渐缩小问题规模的特性解决问题;
通常做法是将问题转化成解空间表达, 然后取中间值与目标进行比较判断, 进而收缩解空间大小, 缩小问题规模;

因此, 二分查找的关键就在于 mid:
nums[mid] 可以将待搜索区间分为两个部分:

  • 一定不存在目标元素的区间: 下一轮搜索的时候, 不用考虑它;
  • 可能存在目标元素的区间: 下一轮搜索的时候, 需要考虑它;

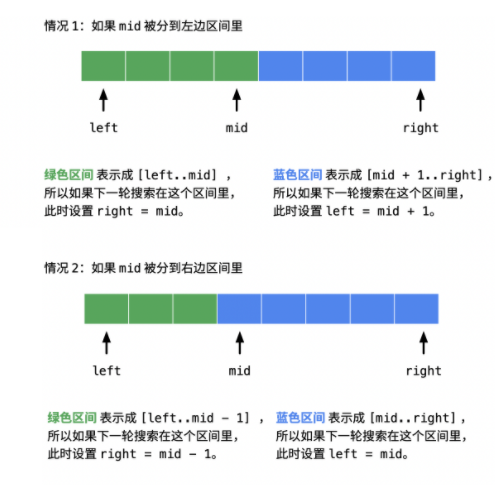
而上述情况中, 又根据 nums[mid] 被划分到哪个区间分为:

  • 如果 mid 分到左边区间, 即区间分成 [left..mid] 与 [mid + 1..right], 此时分别设置 right = mid 与 left = mid + 1;
  • 如果 mid 分到右边区间, 即区间分成 [left..mid - 1] 与 [mid..right], 此时分别设置 right = mid - 1 与 left = mid;

循环条件 [while (left < right)]

此外, 我们把循环条件写成 while (left < right); 这样写的好处在于, 在上面把待搜索区间分成两个部分的情况下, 退出循环以后一定会有 left == right 成立, 因此在退出循环以后, 不需要考虑到底返回 left 还是返回 right;

组织逻辑的「重要的经验」

在写 if 语句的时候, 通常把容易想到的, 不容易出错的逻辑写在 if 的里面;
这样写的依据是: 由于 mid 只划分两个空间, 最终解要么在左区间, 要么在右区间, 我们将不会出错的逻辑写在 if 内, 那么复杂的、容易出错的情况就不用我们去考虑了, 因为它们统统都被包括在了 else 的部分, 这样编写代码不容易出错;

什么情况是容易想到的, 不容易出错的呢?
经验: 题目要我们找符合条件 a 的元素, 我们就对条件 a 取反面, 这样分析不容易出错; 例如题目让我们寻找大于等于 target 的值, 那我们就将小于 target 的值的情况写在 if 内, 因为该情况必然不是正确解, 因此可以收缩解空间范围;

左闭右闭

在二分查找中, 我们实质上始终是在 [left...right] 中搜索解, 通过 mid 将解空间划分成两个区间, 抛弃必不可能存在正解的区间以达到查找目标的结果;
注意: 我们说的是 左闭右闭区间;
为什么不是「左闭右开」呢？
「左闭右开」当然可以, 这是因为任意一个「左闭右开 [left..right) 」区间一定唯一对应一个「左闭右闭 [left..right - 1]」区间, 所以到底是开区间还是闭区间, 前后保持一致就可以;
但是我们不想把精力花在思考「右边界是不是可以取到」这件事情上, 根据 mid 位置是不是目标元素, 进而判断 mid 的左边是否存在目标元素, mid 的右边是否存在目标元素, 只把搜索区间分为两个部分, 然后设置 left 和 right, 在设置 left 和 right 的时候, 左闭右闭区间的形式是最直观的, 这是因为如果是开区间, 还需要在脑子里反应一下, 右端点不包括;

mid 取整方式

在二分查找中, mid 取值通常有以下两种写法:

  • let mid = Math.floor(left + (right - left) / 2);
  • let mid = Math.ceil(left + (right - left) / 2);

第一种写法向下取整, 第二种写法向上取整;

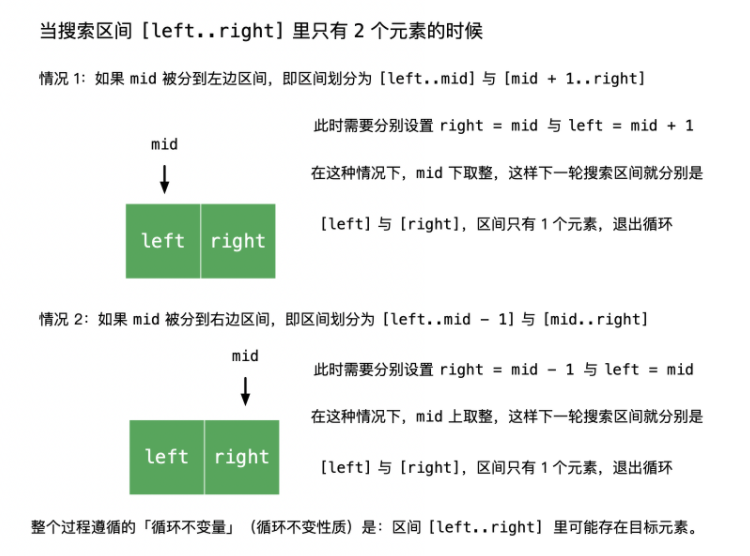
为什么有两种取整方式, 该怎么选择?
是否需要上取整, 只和区间划分的逻辑有关; 如果不调整, 会出现死循环;
由于我们定义的循环条件为 while (left < right), 因此最终必然会有搜索区间 [left...right] 只包含两个元素的情况;

结论: 当区间只剩下两个元素的时候, left = mid 和 right = mid - 1 这种划分方式, 如果 mid 使用默认下取整的方式, 在数值上 left = mid, 而它对应的其中一个区间是 [mid..right], 在这种情况下, 下一轮搜索区间还是 [left..right], 搜索区间没有减少, 会进入死循环;

提示: 「看到边界设置的代码是 left = mid 时, 需要把 mid 的取法调整为上取整, 以避免死循环」, 「看到边界设置的代码是 right = mid 时, 需要把 mid 的取法调整为下取整, 以避免死循环」;
记忆: 当 left = mid 时, 由于我们要避免 mid 落入 left 中, 因此计算时通过向上取整, 让每次 mid 计算都落入 right, 然后通过 right = mid - 1 来跳出循环; right = mid 同理;

总结

  1. 首先想清楚这道问题为什么可以用二分查找解决(而不应该先纠结二分查找该怎么写), 利用题目中给出的单调性或者可以缩减问题规模的特点：已知某个猜测的答案的结果, 就可以推测出比当前猜测小的时候结果如何, 比当前猜测大的时候结果如何; 常见应用为：有序或者半有序数组中找下标, 确定一个有范围的整数;
  2. 首先确定搜索的范围(解空间), 如果搜索的范围就把正确答案排除在外, 那么是无论如何也搜不出正确结果的；
  3. 可以从「看到的中间元素什么时候不是解」开始思考 if 的语句怎么写, if 的逻辑越简单越好, 这样才能保证不会错, 剩下的复杂的情况留给 else, else 的区间就是剩下的区间；
  4. 只把区间分成两个部分, 代码也写成两个部分, 这样, 在 while (left < right) 的循环体退出以后, left == right 才成立（理解这一点非常重要, 理解的基础是做适当的练习, 进行必要的调试）；
  5. 看到 if 和 else 里有 left = mid 的时候, 需要将 mid 调整为上取整, 原因是当区间里只剩下两个元素的时候, mid 看到右边元素, 这样落入 left = mid 的时候, 区间才会缩减; 如果觉得这一点很难理解的朋友, 打印变量看一下就非常清楚了；
  6. 如果搜索区间里一定存在目标元素, 退出 while (left < right) 以后, 返回 left 或者 left 代表的值就可以, 否则还需要单独做一次判断；

练习

704. 二分查找


题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var search = function (nums, target) {
  // 初始化解空间 [0, nums.length-1]
  let left = 0;
  let right = nums.length - 1;

  // 二分查找: 当 left === right 时跳出循环;
  // left < right 优势: 最终得到结果时, 不需要考虑取 left 还是 right;
  while (left < right) {
    // 获取 mid 索引;
    // 由于后续 left = mid, 因此此处 mid 向上取整, 避免只剩两个元素时 mid 落入 left 后发生死循环(向上取整, 落入 right, right 可以通过 - 1 跳出循环)
    let mid = Math.ceil(left + (right - left) / 2);
    if (nums[mid] > target) {
      right = mid - 1;
    } else {
      left = mid;
    }
  }
  return nums[left] === target ? left : -1;
};

34. 在排序数组中查找元素的第一个和最后一个位置


题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var searchRange = function (nums, target) {
  // 问题 <=> 寻找左边界和右边界

  // 将寻找边界写成一个函数, findLeft 控制寻找左边界或右边界
  function find(nums, target, findLeft = true) {
    // 初始化解空间 [0, nums.length-1]
    // 解空间建议采用左右闭区间, 这样就不需要考虑左开或右开导致的问题, 更符合人的思维方式;
    let left = 0;
    let right = nums.length - 1;

    // 二分查找
    while(left < right) {
      if (findLeft) {
        // 寻找左边界
        let mid = Math.floor(left + (right - left) / 2);
        // 当 mid 对应值比目标值小时, 说明左侧包括 mid 均不符合;
        // 二分法将整个解空间划分为了两个区间, 我们只需要判断值落在哪个区间, 并舍弃另一区间即可; 下述代码等价于将解空间划分为 [left...(mid)] [(mid + 1)...right];
        // 小技巧: 通常将不容易出错的逻辑写在 if 内, 这样正解必然包含在 else 内, 无需我们判断;
        if (nums[mid] < target) {
          left = mid + 1
        } else {
          right = mid
        }
      } else {
        // 与上述思路相同, 寻找右边界, 只不过 mid 要向上取整, 避免 mid 落入 left 中发生死循环;
        let mid = Math.ceil(left + (right - left) / 2);
        if (nums[mid] > target) {
          right = mid - 1
        } else {
          left = mid;
        }
      }
    }
    return nums[left] === target ? left : -1
  }

  return [find(nums, target, true), find(nums, target, false)]
};

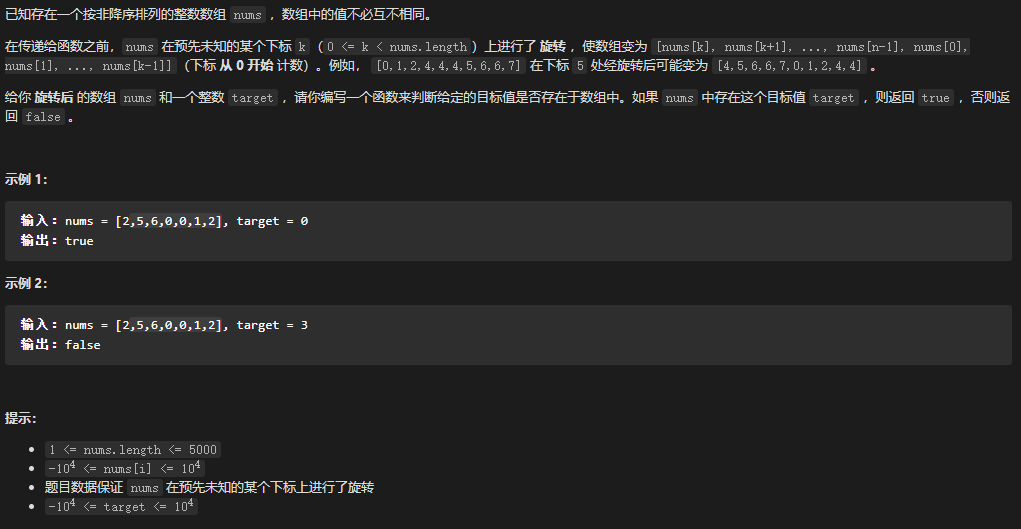
33. 搜索旋转排序数组


题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var search = function (nums, target) {
  let left = 0;
  let right = nums.length - 1;

  while (left < right) {
    let mid = Math.floor(left + (right - left) / 2);
    // 旋转数组首先要通过 mid 判断有序数组;
    // 当 mid 对应值 > left 对应值时, 说明 [left...mid] 是有序的; 反之, 说明 [mid...right] 是有序的;
    // nums[mid] == nums[left] 处理和 > 一样, 因此写到一起;
    if (nums[mid] >= nums[left]) {
      // 当解空间 [left...mid] 有序时, 判断 target 和边界, 从而确定 target 是在该有序解空间内还是外, 从而缩小解空间范围;
      if (target >= nums[left] && target <= nums[mid]) {
        right = mid
      } else {
        left = mid + 1
      }
    } else {
      // 因为 mid 是向下取整的, 所以我们要保证 right = mid, 即 mid 每次都要落在 right 上; 所以这里的判断条件是 target 是否在 (mid, right] 内, 这样才能保证 left = mid + 1;
      if (target > nums[mid] && target <= nums[right]) {
        left = mid + 1
      } else {
        right = mid;
      }
    }
  }

  return nums[left] === target ? left : -1;
};

81. 搜索旋转排序数组 II


题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var search = function(nums, target) {
  // 旋转数组 - 有重复值版本
  let left = 0;
  let right = nums.length - 1;
  
  while(left < right) {
    let mid = Math.floor(left + (right - left) / 2);

    // 只需要在原先旋转数组基础上改进一点即可
    // 当 nums[mid] === nums[left] === nums[right] 时, 此时无法判断有序序列, 因此只需要跳过该情况, 两端同时收缩区间即可;
    if (nums[left] === nums[mid] && nums[mid] === nums[right] && right - left > 1) {
      left += 1;
      right -= 1;
      continue;
    }

    // 同 33.旋转数组
    if (nums[mid] >= nums[left]) {
      if (target >= nums[left] && target <= nums[mid]) {
        right = mid
      } else {
        left = mid + 1;
      }
    } else if (nums[mid] < nums[left]) {
      if (target > nums[mid] && target <= nums[right]) {
        left = mid + 1;
      } else {
        right = mid;
      }
    }
  }

  return nums[left] === target;
};

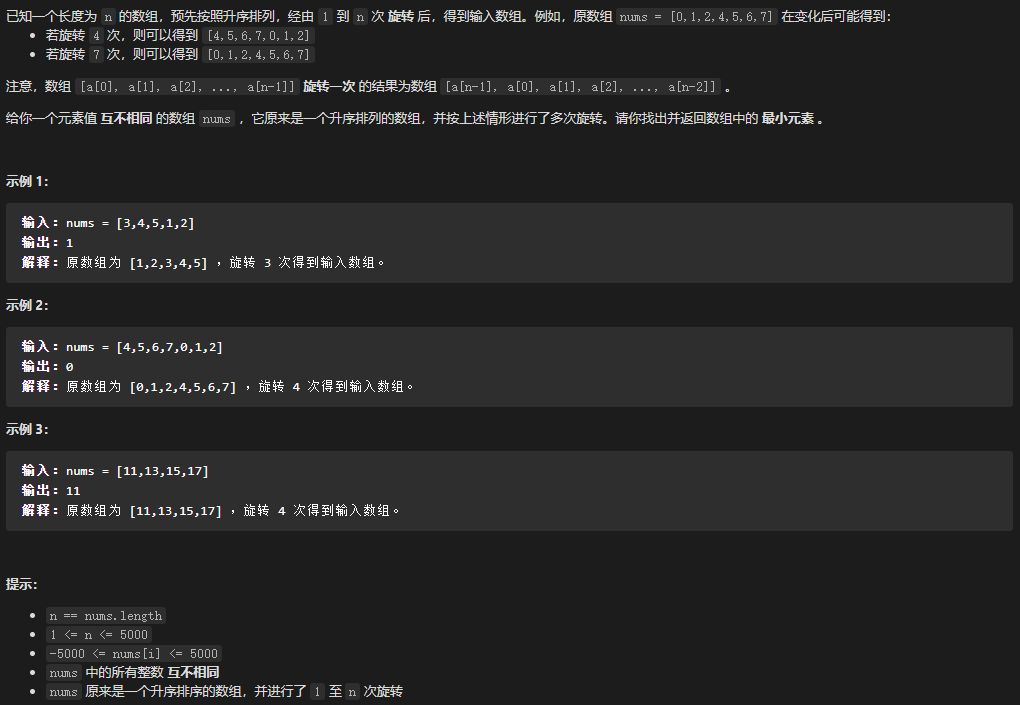
153. 寻找旋转排序数组中的最小值


题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var findMin = function (nums) {
  // 旋转数组可以画一个单调性的图, 通过观察可知, 当 mid 大于右边界时, 说明最小值存在于右侧 [(mid+1)...right], 反之最小值存在于左侧区间 [left...mid]
  let left = 0;
  let right = nums.length - 1;

  while (left < right) {
    let mid = Math.floor(left + (right - left) / 2);
    if (nums[mid] > nums[right]) {
      left = mid + 1
    } else {
      right = mid;
    }
  }

  return nums[left];
};

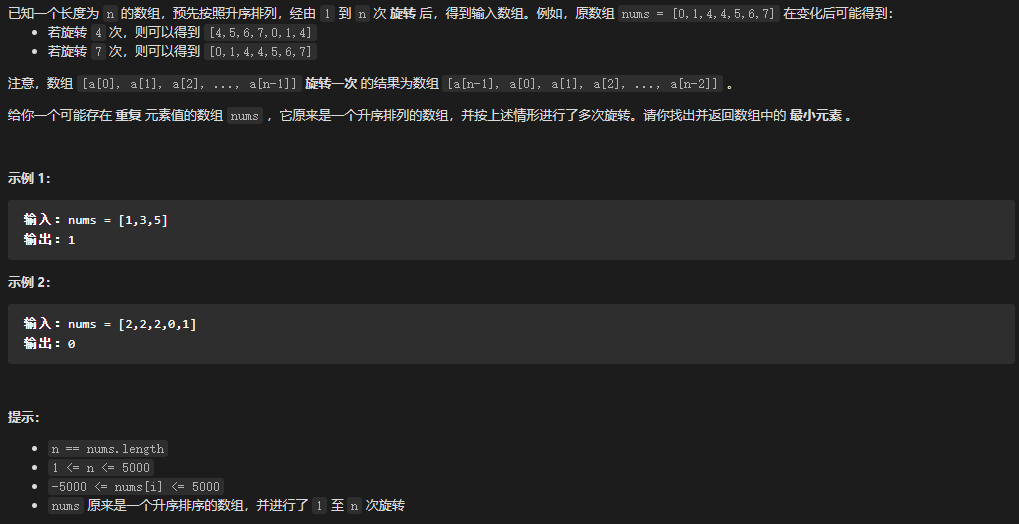
154. 寻找旋转排序数组中的最小值 II


题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
var findMin = function(nums) {
  let left = 0;
  let right = nums.length - 1;

  while(left < right) {
    let mid = Math.floor(left + (right - left) / 2);

    // 旋转数组重复值就用该方法解决;
    // 当遇到 mid = left = right 值相同时, 此时无法判断有序数组在哪一部分, 两端缩进, 跳过;
    if (right - left > 1 && nums[left] === nums[mid] && nums[mid] === nums[right]) {
      left += 1;
      right -= 1;
      continue
    }

    // 后续思路同不重复旋转数组一样; 当作没有重复值的旋转数组来解决;
    if (nums[mid] > nums[right]) {
      left = mid + 1
    } else {
      right = mid;
    }
  }

  return nums[left];
};

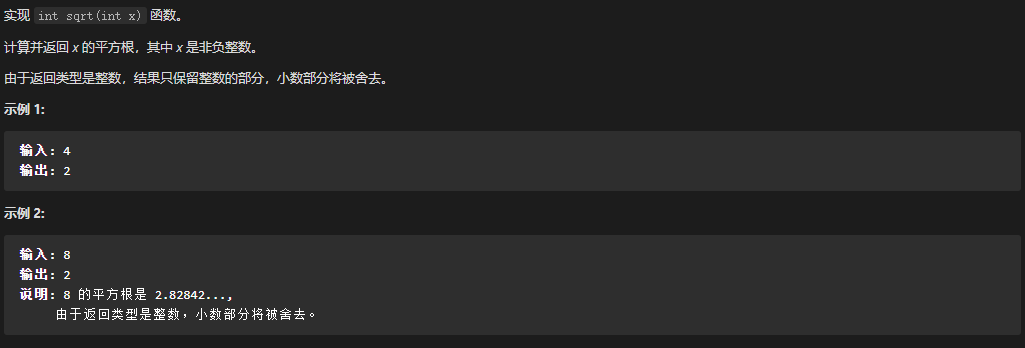
69. x 的平方根


题解:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var mySqrt = function(x) {
  if (x === 0) return 0;
  if (x === 1) return 1;

  let left = 1;
  let right = Math.ceil(x/2);

  while (left < right) {
    let mid = Math.ceil((left + right) / 2);
    if (mid**2 > x) {
      right = mid - 1;
    } else {
      left = mid;
    }
  }
  return left;
};